Luc Schnell
PhD Student in Theoretical Particle PhysicsI am a PhD student at the Max Planck Institute for Physics and the Technical University Munich. My current interests lie in collider phenomenology, including beyond the SM (BSM) signals, Monte Carlo tools and QCD corrections.
Recently, I have focussed on calculating higher-order corrections to the signals of SM Effective Field Theory (SMEFT) operators and of specific new physics UV models at the LHC. In this context, I created (N)NLO+PS accurate event generators based on the POWHEG and MadGraph_aMC@NLO frameworks.
I am supervised by Ulrich Haisch.
1997
YEAR OF BIRTH
SWITZERLAND
NATIONALITY
GERMAN (NATIVE), ENGLISH (C2), FRENCH (C1)
LANGUAGE
Research (selection)
2023
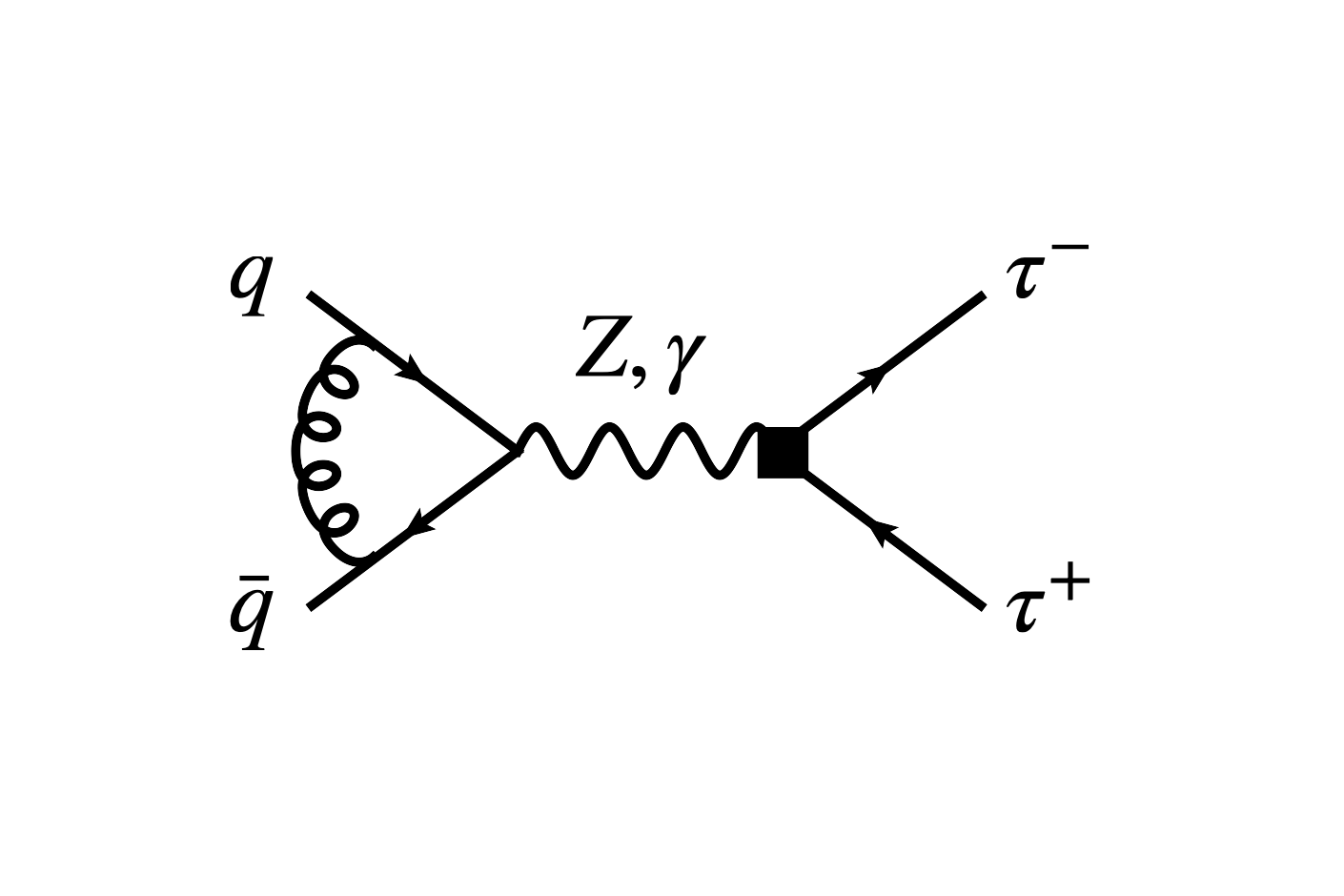
LHC tau-pair production constraints on atau and dtau
Ulrich Haisch, LS, Joachim Weiss
2023
Long-lived particle phenomenology in the 2HDM+a model
Ulrich Haisch, LS
2022
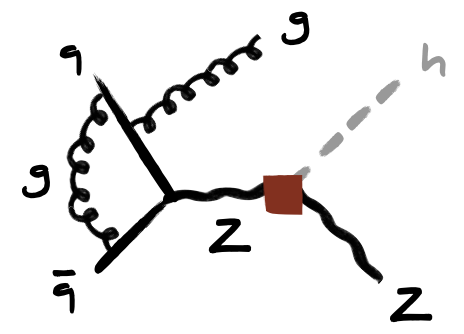
Drell-Yan production in third-generation gauge vector leptoquark models at NLO+PS in QCD
Ulrich Haisch, LS, Stefan Schulte
2022
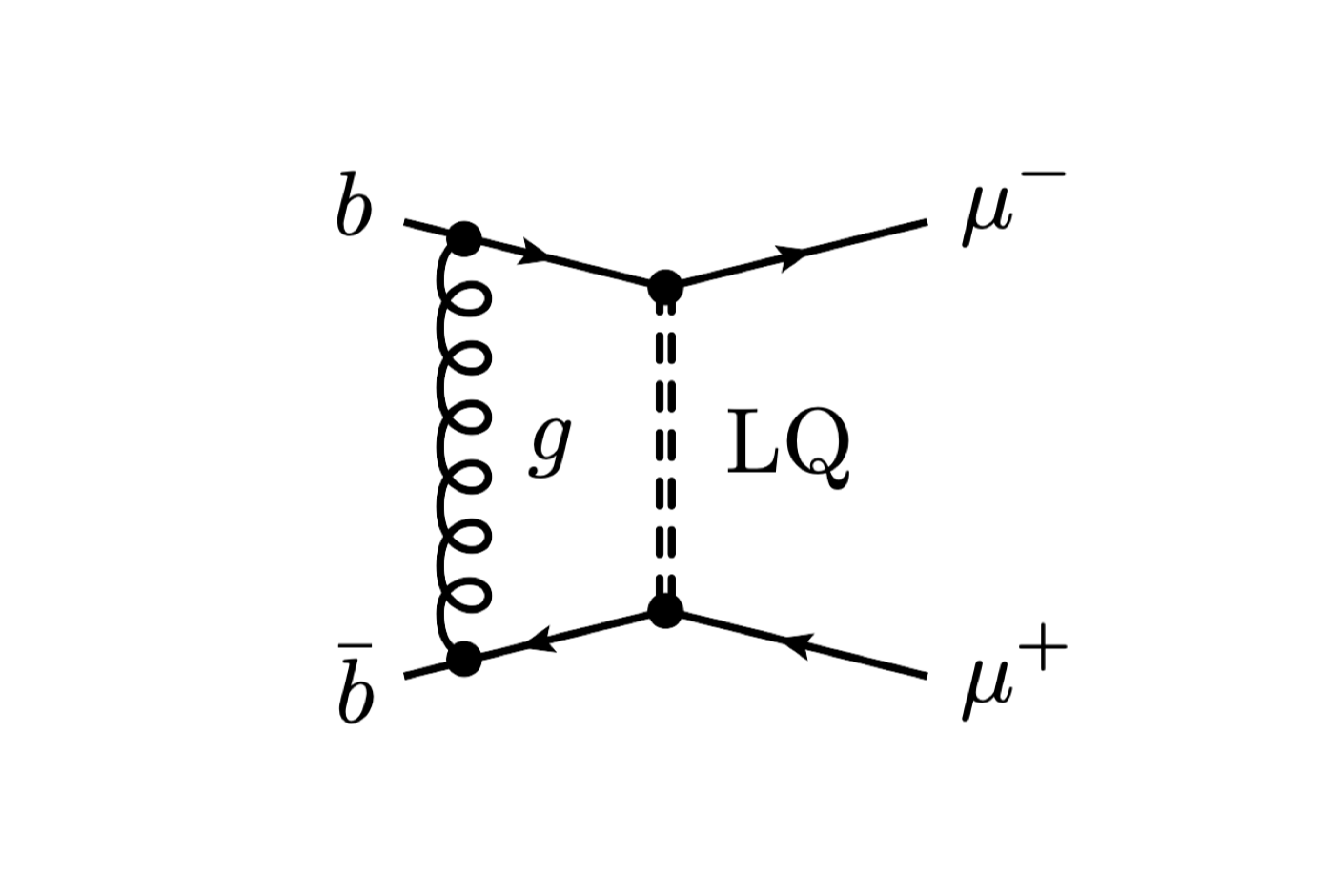
On Drell-Yan production of scalar leptoquarks coupling to heavy-quark flavours
Ulrich Haisch, LS, Stefan Schulte
2022
Explaining the hints for lepton flavour universality violation with three S2 leptoquark generations
Andreas Crivellin, Benjamin Fuks, LS
2021
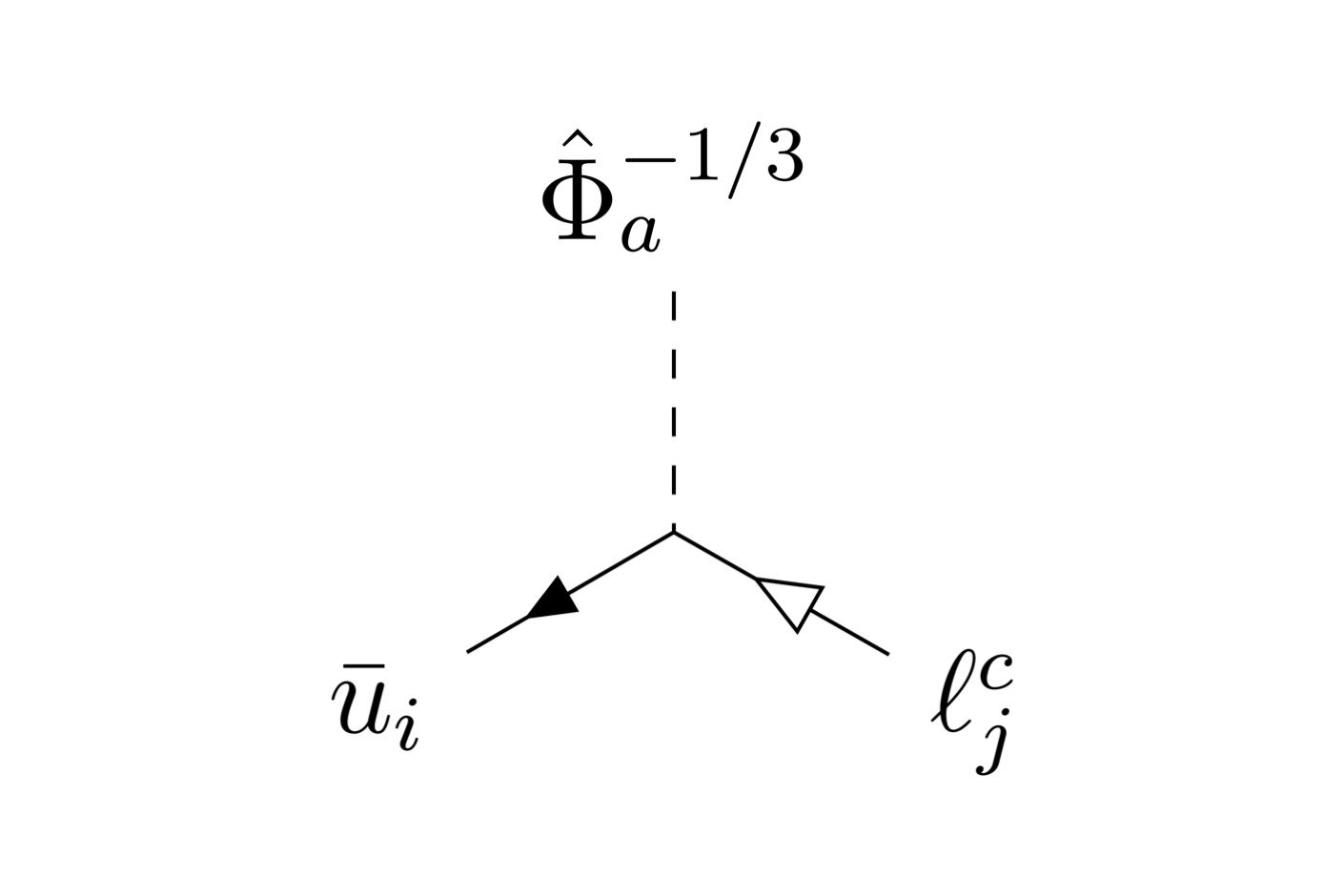
Complete Lagrangian and Set of Feynman Rules for Scalar Leptoquarks
Andreas Crivellin, LS
2021
First-Generation New Physics in Simplified Models: From Low-Energy Parity Violation to the LHC
Andreas Crivellin, Martin Hoferichter, Matthew Kirk, Claudio Andrea Manzari, LS
Extracurriculars
Swiss Physics Olympiad
Board member. Secretary. Part of the editorial team.Research Science Institute
Alumni. Organizing the participation of the Swiss candidate in the Research Science Intitute at MIT.Blogging
I write about more topics that interest me on my blog meonworld.com.
Contact
Email
schnell@mpp.mpg.de
schnell@mpp.mpg.de
Skype
luc.schnell
luc.schnell